Em 1900, David Hilbert, um dos matemáticos mais influentes da história, fez 23 perguntas que moldariam o futuro da matemática. Dentre eles, o problema 16 se destaca como um dos problemas mais desafiadores, resolvendo o interessante problema dos ciclos limites em sistemas dinâmicos descritos por equações diferenciais polinomiais. Depois de mais de um século sem solução, os pesquisadores da Universidade Estadual de São Paulo (UNESP) Dr. Vinícius da Silva, Dr. João Vieira e Professor Edson Denis Leonel descobriram uma solução utilizando uma abordagem inovadora baseada na geometria da informação. Suas descobertas foram publicadas na revista entropia.
Qual é a 16ª pergunta de Hilbert?
A questão pode ser dividida em duas partes. A primeira envolve curvas elípticas no plano cartesiano, enquanto a segunda é mais complexa e visa determinar o número máximo e a localização de ciclos limites em um sistema dinâmico de polinômios de grau n.
Um ciclo limite representa uma trajetória fechada e isolada em um sistema que se repete infinitamente, como as oscilações de um pêndulo ou o comportamento de um circuito elétrico. Estes ciclos são cruciais para simular fenómenos naturais e artificiais, desde ritmos biológicos até sistemas de comunicação.
Apesar das inúmeras tentativas, uma solução completa permanece indefinida. Os métodos tradicionais identificaram ciclos limites, mas não conseguiram determinar o seu número ou localização precisa.
A descoberta do Brasil
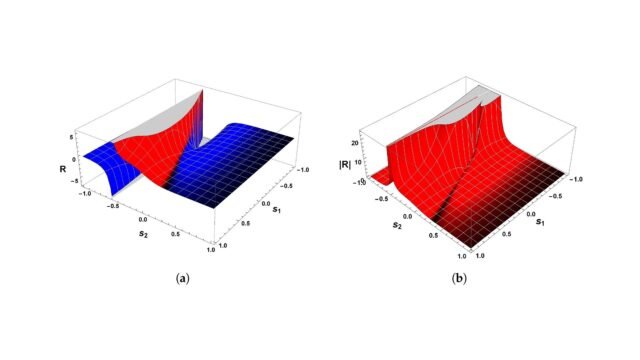
Para superar dificuldades comuns na pesquisa de ciclos limites, o Dr. Vinícius Barros da Silva, o Dr. João Peres Vieira e o professor Edson Denis Leonel introduziram a teoria da bifurcação geométrica (GBT), um método avançado que combina geometria e dinâmica para analisar mudanças no sistema. Usando a curvatura escalar Riemanniana, os pesquisadores descobriram que o número máximo de ciclos limites está diretamente relacionado à curvatura divergente para o infinito.
Da Silva disse: “A teoria da bifurcação geométrica revela não apenas o número de ciclos limites, mas também suas localizações. Nosso estudo mostra que esses padrões repetidos estão relacionados ao comportamento da curvatura escalar do sistema. Mais precisamente, quando a curvatura é positiva e atinge um valor extremo, indica o número máximo de ciclos limites que um determinado sistema dinâmico pode ter. “
Esta inovação foi demonstrada em mais de 20 sistemas dinâmicos, variando desde configurações simples com poucos ciclos limites até sistemas altamente complexos com muitos ciclos limites. Os resultados são obtidos sem depender de métodos de perturbação, destacando a robustez e versatilidade do método.
“Até o momento, nosso trabalho recebeu mais de 4.500 visualizações em menos de três meses e recebeu inúmeras sugestões de pesquisadores de todo o mundo, enfatizando ainda mais a confiabilidade e o impacto das descobertas. O amplo apoio da comunidade científica enfatiza a importância e a consistência da nossa solução”, acrescentaram o Dr.
Impacto e aplicação
A descoberta do Brasil não apenas resolve um problema matemático centenário, mas abre portas para aplicações práticas. Os ciclos limites são ferramentas poderosas para modelar e prever o comportamento em vários campos, como a biologia para compreender a dinâmica populacional ou a engenharia para desenvolver sistemas de controle mais eficientes. Além disso, o GBT tem o potencial de revolucionar campos como a segurança cibernética e a criptografia quântica, onde os ciclos de limite podem ser usados para criar sistemas de comunicação e segurança mais robustos.
Os investigadores pretendem agora estender as suas descobertas a sistemas dinâmicos de dimensões superiores que envolvem mais variáveis e interações complexas, como as encontradas na mecânica quântica e nas redes neurais.
Marcos na História da Matemática
Ao unir os conceitos de geometria e dinâmica, a solução brasileira para o 16º problema de Hilbert é um excelente exemplo de como a matemática está mudando nossa compreensão do universo e fornecendo ferramentas práticas para resolver desafios científicos e tecnológicos.
No total, este trabalho inovador resolve o 16º problema de Hilbert, ao mesmo tempo que destaca o potencial da geometria para desbloquear respostas em muitos campos. Ao assumir uma nova perspectiva sobre um problema antigo, a equipe não apenas dominou a matemática avançada, mas também mostrou como esse conhecimento pode ser aplicado a sistemas do mundo real.
Palavras-chave: Ciclos limites, sistemas dinâmicos, David Hilbert, teoria da bifurcação geométrica, matemática aplicada.
Referência do diário
da Silva, VB, Vieira, JP e Leonel, ED “Explorar ciclos limites de equações diferenciais através da geometria da informação revela soluções para o 16º problema de Hilbert.” Entropia, 2024, 26, 745. doi: https://doi.org/10.3390/e26090745
Sobre o autor
Dr. Vinícius Barros Possui doutorado. Em 2023, recebeu seu doutorado em Física Aplicada pela Universidade Estadual de São Paulo “Júlio de Mesquita Filho” (UNESP), Brasil. Antes disso, obteve mestrado pela UNESP em 2018 e bacharelado em física pela mesma instituição. Em 2018, o Dr. Vinícius atuou como pesquisador visitante no Istituto dei Sistemi Complessi (ISC), Consiglio Nazionale delle Ricerche, Itália. Dr. Vinícius também recebeu reconhecimento notável por suas realizações acadêmicas, incluindo o primeiro lugar no Programa de Pós-Graduação da UNESP 2019, doutorado. Além disso, foi eleito melhor aluno da turma de ingresso no curso de Física da UNESP em 2018 e foi reconhecido pelo excelente desempenho acadêmico no curso de Física da UNESP no mesmo ano.
Seus interesses de pesquisa cobrem uma ampla gama de tópicos em física, incluindo sistemas dinâmicos, caos, geometria da informação de Fisher, geometria diferencial, métricas de Fisher e Rao, curvatura escalar e teoria da bifurcação. O trabalho do Dr. Barrows em física estatística, geometria da informação e sistemas dinâmicos visa fazer contribuições significativas para o avanço do conhecimento nessas áreas.
Ele busca uma posição de pós-doutorado ou professor associado para continuar sua jornada científica.

Dr. João Pérez Vieira Obteve seu bacharelado em matemática pela Universidade Federal de São Carlos em 1984, seu mestrado em matemática pela Universidade de São Paulo em 1988 e seu doutorado em matemática pela Universidade de São Paulo em 1988. Em 1995, obteve seu doutorado em Matemática pela mesma instituição. Em 2012 formou-se em Matemática pela Universidade Estadual Paulista “Júlio de Mesquita Filho”, onde atualmente atua como Professor Associado.
Dr. Vieira possui amplo conhecimento matemático, especializando-se em topologia algébrica e sistemas dinâmicos. Os seus principais interesses de investigação centram-se em pontos fixos, teoria da correspondência e suas aplicações em dinâmica topológica, fornecendo informações importantes sobre o comportamento e a estrutura de sistemas dinâmicos complexos. Suas contribuições refletem um forte compromisso com o avanço da compreensão dos aspectos teóricos e aplicados dessas áreas da matemática.

Dr. Edson Dennis Lionel é professor titular do Departamento de Física do Campus Rio Claro da Universidade Estadual Paulista (UNESP). Possui bacharelado (1997), mestrado (1999) e doutorado em física pela Universidade Federal de Viçosa. Doutor em Física pela Universidade Federal de Minas Gerais (2003). Dr. Edson Denis Leonel concluiu sua formação no Instituto de Geociências e Ciências Exatas (IGCE) da UNESP em 2009 e realizou pesquisa de pós-doutorado na Lancaster University (2003-2005). Em 2009, atuou como professor visitante na Georgia Tech.
Com experiência em caos e sistemas dinâmicos, sua pesquisa se concentra em análise de séries temporais, leis de escala, mapas discretos, dinâmica caótica, aceleração de Fermi, bilhar clássico e autômatos celulares. Ele recebeu o Prêmio V. Afraimovich em 2023 da Conferência Internacional sobre Ciência Não Linear e Complexidade. Como educador dedicado, contribuiu para programas de graduação e pós-graduação. Além disso, atuou como Vice-Presidente do Instituto de Geociências e Ciências Exatas (IGCE) de 2017 a 2021 e atualmente é Presidente (2021-2025).